Summation
Summation in mathematics is denoted by a capital letter sigma Σ.
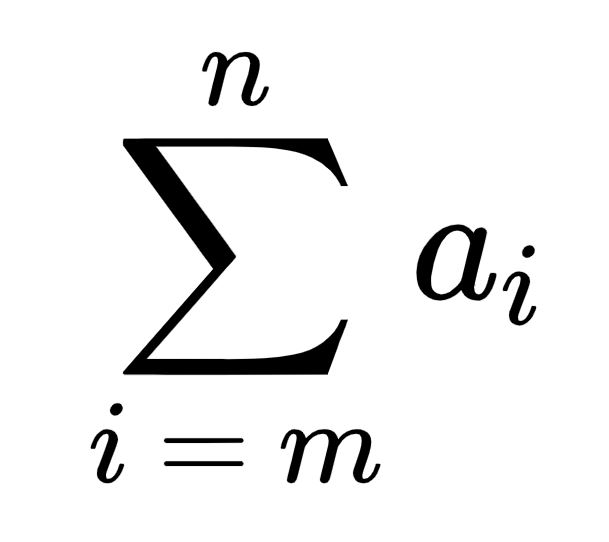 ai – indexed variable
ai – indexed variable
i – index of summation
n – upper bound of summation
m – lower bound of summation
Summation examples
Let's sum the natural numbers from 1 to 10, then m = 1, n = 10.
=
=
Calculate the sum of fractions, where an indexed variable = , lower bound of summation = 1, upper bound of summation = 5. If the summation index can be any variable, then instead of i we use the index n in this example.
=
=
=
Now let's write as an indexed variable an expression that, in addition to the summation index, contains other variables. Compute the sum, where an indexed variable = , lower bound of summation = 1, upper bound of summation = 4.
=
=
Let's take another example. Compute the sum, where an indexed variable = , lower bound of summation = -2, upper bound of summation = 3.
=
=
=
Infinite Series
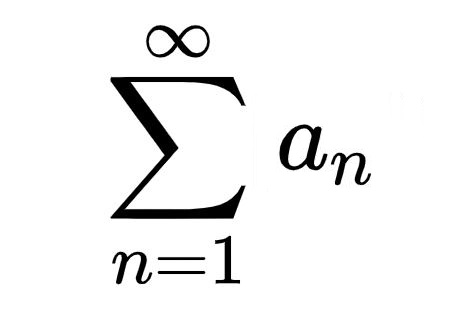 an – indexed variable
an – indexed variable
n – index of summation
∞ – upper bound of summation
1 – lower bound of summation
The sum of an infinite number of terms, also called the sum of the series - is a mathematical expression with which you can write an infinite number of terms.
If the limit of the terms of the sum is equal to a finite number, then such a series is called convergent.
If the limit of the terms of the sum does not exist, or it is equal to infinity, then such a series diverges and is called divergent.
For example, the harmonic series is divergent:
=
The series is divergent